关押罪犯

题目链接(luogu)

tzhsoj

文章大意： n个点间有m条边，每条边上都有着对应的权值，现要求将这n个点分为两个集合，要求两个集合 内部 的最大边 最小 ，若无边则输出0

由于求最大边最小，所以显然贪心(及将边权从大到小排列)

解法一：种类并查集

首先先了解什么是种类并查集；它是拓展域并查集的一种；

拓展域便是将原本并查集的空间拓展整数倍，此时原本一倍的空间就不够用了

在种类并查集中，在同种类的集合中合并与原来没有什么区别，及他们是朋友

而在不同种类的集合中合并则表示两者间的对立关系，例如他们之间是敌人

种类的说法其实不够准确，它更像是关系； 例如：

1. 敌人的敌人是朋友
2. 捕食关系(吃别人)、同类关系、天敌关系(被吃)洛谷P2024 食物链

；常见的是两倍，例如这题。

本题由于只分为两个集合，类似于只有朋友和敌人两个关系，怎么类似的呢？

首先假设我们已经将最大边权的两点放入两个集合(记为左右集合)中，此时出现了第3个点，他与其中一个点(设为点1处于左集合)有边，为了避免他们间发生矛盾(即该条边在同一个集合内)，我们将其放入另一个集合内(也就是右集合)，与点2放置在一起，不就是类似于敌人的敌人是朋友的关系了吗？

抽象符号：

∵1 <=> 2 & 1 <=> 3   ∴  2 === 3

详细点，举样例说： 先排序得到：

1 - 2 28351

3 - 4 12884

1 - 3 6618

2 - 3 3512

1 - 4 2534

2 - 4 1805

我们先将1，2扔进不同的两个集合里，但是我们不能保证1一定在左集合，2一定在右集合，因此，我们可以将两者一起考虑，也就是把左集合中的1和右集合中的2合并 ， 右集合中的1和左集合的2合并，能够得到如图的关系 有水印是因为这是我从自己洛谷博客上扒的(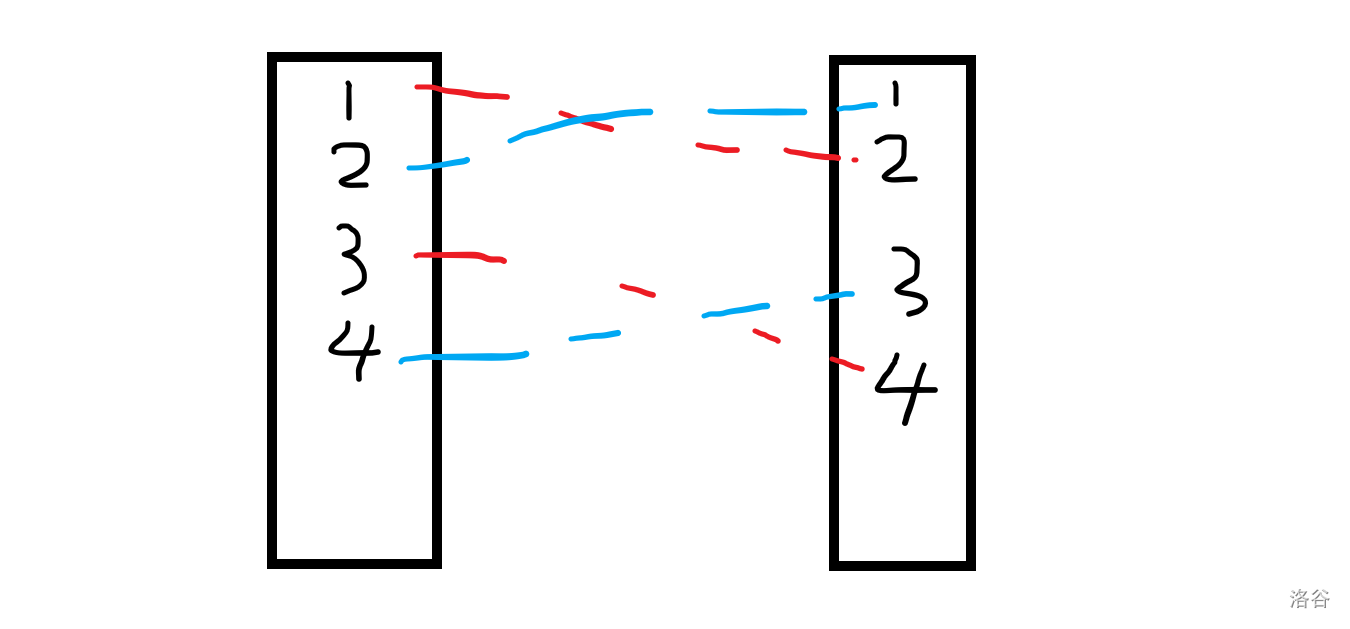

接着考虑1 - 3，为了避免冲突，显然我们会将2、3放在同一个集合中。

以此类推，到2 - 3 时刚刚好矛盾发生，此时的矛盾值就是最大的了，不难得出代码。

#include <bits/stdc++.h>
#define int long long int

using namespace std;

const int N = 2e5 + 7;
int n,m,effect;
int fa[N << 1];

struct node{
	int val; 
	int nex,to;
}e[N];

bool cmp(node a1,node a2){
	return a1.val > a2.val;
}

inline int read(){
	int x = 0,f = 1;
	char c = getchar();
	for(;!isdigit(c);c = getchar())
		if(c == '-')f = -1;
	for(;isdigit(c);c = getchar())
		x = (x << 1) + (x << 3) + c - '0';
	return x * f;
}

int get(int x){
	if(fa[x] == x)return x;
	return fa[x] = get(fa[x]);
}

void merge(int x,int y){
	x = get(x);
	y = get(y);
	fa[x] = y;
}

signed main(){
	n = read();m = read();
	
	for(int i = 1;i <= n;i ++){
		fa[i] = i;fa[i + n] = i + n;
	}
	
	for(int i = 1;i <= m;i ++){
		e[i].nex = read();
		e[i].to = read();
		e[i].val = read();
	}
	
	sort(e + 1,e + 1 + m,cmp);
	
	for(int i = 1;i <= m;i ++){
		int x = e[i].nex,y = e[i].to;
		if(get(x) == get(y) || get(x + n) == get(y + n)){
			effect = e[i].val;
			break;
		}
			
		merge(x + n,y);
		merge(x,y + n);
	}
	
    printf("%lld",effect);
	
	return 0;
}

最大耗时48ms

解法二: 朴素的根据敌人的敌人合并

当然，也是先排序，按边加，直至第一次发现冲突退出

#include <bits/stdc++.h>
#define int long long int

using namespace std;

const int N = 2e5 + 7;
int n,m,effect;
int fa[N << 1],e[N];
struct node {
    int nex,to,val;
}edge[N];


inline int read(){
	int x = 0,f = 1;
	char c = getchar();
	for(;!isdigit(c);c = getchar())
		if(c == '-')f = -1;
	for(;isdigit(c);c = getchar())
		x = (x << 1) + (x << 3) + c - '0';
	return x * f;
}

bool cmp(node a1,node a2){
    return a1.val > a2.val;
}

int get(int x){
	if(fa[x] == x)return x;
	return fa[x] = get(fa[x]);
}

void merge(int x,int y){
	x = get(x);
	y = get(y);
	fa[x] = y;
}

signed main(){
	n = read();m = read();
	
	for(int i = 1;i <= n;i ++){
		fa[i] = i;
	}
	
    for(int i =1 ;i <= m;i ++){
        edge[i].nex = read();
        edge[i].to = read();
        edge[i].val = read();
    }

    sort(edge + 1,edge + 1 + m,cmp);

	for(int i = 1;i <= m;i ++){
		int x = edge[i].nex,y = edge[i].to;
       		if(get(x) == get(y)){
            	effect = edge[i].val;
            	break;
        	}
		if(!e[x]) e[x] = y;
		else{
		merge(e[x],y);
		}
		if(!e[y]) e[y] = x;
		else{
			merge(e[y],x);
		}
		
	}
	
    printf("%lld",effect);

	return 0;
}

最大耗时54ms

点我博客食用更佳

这题的数据好像不是很水，所以最大的一个点跑了50+ms

关押罪犯

（PS：部分前置知识在博客的笔记里）

众所周知，一般而言，随着经济社会的发展...

（以上省略114514字）...今天，小编就来给大家带来 关押罪犯 的...

对于这道题，我们要使最大怨气的事件尽可能小，所以我们对输入的关系图按照怨气降序进行排序。

我们用ene[i]储存i的敌人序号。对于每对罪犯，我们应该尽可能将他们分到两个监狱。

如果他们可以被安排下去的话，即两位的阵营祖先不是同一个，就把他的敌人设成后面一位。如果前面有的话，那就认贼作父，将其敌人的父节点设为自己的祖先。

但如果不能安排下去，就直接输出当前的怨气值，然后关闭程序。

以下代码：

#include <bits/stdc++.h>
using namespace std;

struct ppp{int a,b,c;}mn[100010];

int n,m,t,ans;
int fa[30000],ene[30000];

bool cmp(ppp l,ppp r){return l.c>r.c;}

int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}

signed main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>mn[i].a>>mn[i].b>>mn[i].c;
    }
    sort(mn+1,mn+m+1,cmp);
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<=m;i++){
        int fx=find(mn[i].a),fy=find(mn[i].b);
        if(fx==fy){cout<<mn[i].c;return 0;}
        if(!ene[mn[i].a])ene[mn[i].a]=mn[i].b;
        else fa[find(ene[mn[i].a])]=find(mn[i].b);
        if(!ene[mn[i].b])ene[mn[i].b]=mn[i].a;
        else fa[find(ene[mn[i].b])]=find(mn[i].a);
    }
    cout<<0;
    return 0;
}